Retrying principal component analysis and gaussian mixture models
We create a simpler dataset and use principal component analysis (PCA) and gaussian mixture models (GMMs) over this dataset.
The simpler dataset
First, we modify our data processing script (1) to create a small dataset, (2) with just two classes. The first class is the BENIGN class (label 0), and the second is the PortScan class (label 11). Both classes have 8,000 samples for a total of 16,000 rows in the dataset.
The main idea here is to reduce the complexity of visualizing multiple classes in the same chart. We hope that the simplification will improve our understanding of the features in the data.
Dimensionality reduction with PCA
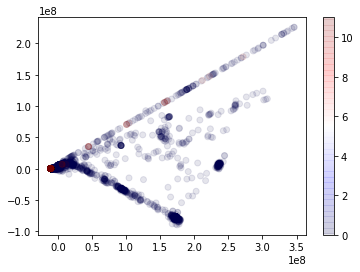
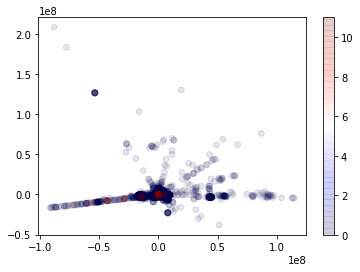
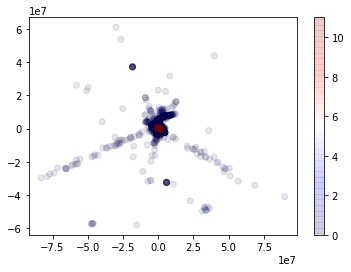
Next, we reduce the dimensionality of the data using PCA (3) and plot the actual labels (as colors) against the principal components (two components at a time). We see that the BENIGN class (regular traffic on the network) has a lot more variability than the PortScan class (where an attacker uses a software tool to probe servers for open ports). Intuitively, the variability observation makes sense as the natural traffic on a network encompasses many different applications and user types. Attackers typically seek to hide their traffic within this natural variability.
Principal components one, two
Principal components three, four
Principal components five, six
Sanity check with logistic regression
Logistic regression can separate out the two classes with 99%+ accuracy (on a test set, separate from the training set; there is no validation set in this experiment). This is a quick sanity check that confirms that the dataset is (mostly) separable and that the data processing steps have not mangled the features.
GMMs do not fit
Finally, we fit a GMM against an unlabeled version of the dataset. We find that GMM badly under-fits, assigning 2,452 samples to one class and 13,548 to the other. A great fit would find ~8,000 samples for both classes. At least in the case of the two-class dataset, we conclude that GMM is not a reasonable method to discover the structure of the CICIDS2017 data.